Grundlagen der Messunsicherheit
Diese Wissensseite beantwortet Fragen zur Bedeutung, Relevanz, Auswirkung, Bestimmung und zur Berechnung der Messunsicherheit. In diesem Zusammenhang erhalten Sie Informationen zum Sensitivitätskoeffizient und der Messunsicherheitsbilanz/-budget.
Hier finden Sie Antworten auf die folgenden Fragen:
- Was bedeutet Messunsicherheit?
- Zusammenhang zwischen: Präzision, Genauigkeit und Auflösung
- Warum ist die Messunsicherheit relevant?
- Welche Auswirkung hat die Messunsicherheit im Rahmen der Kalibrierung?
- Wie wird die Messunsicherheit bestimmt und berechnet?
- Was bedeutet Messunsicherheit nach GUM?
- Statistische Grundlagen für die Messunsicherheitsberechnung
- Was bedeutet Sensitivitätskoeffizient im Rahmen der Messunsicherheit?
- Was ist eine Messunsicherheitsbilanz/Messunsicherheitsbudget?
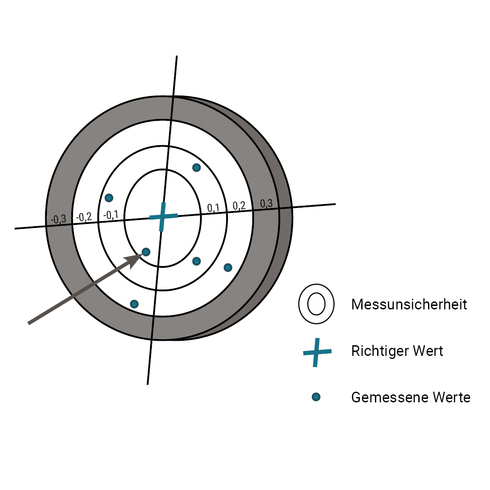
Was bedeutet Messunsicherheit?
Messungen liefern keine absolut genauen Werte, da sie stets Unzulänglichkeiten und Unvollkommenheiten unterliegen, die nicht genau quantifiziert werden können. So ist das Ergebnis einer Messgrösse von dem angewandten Messverfahren, den Umgebungsbedingungen wie Temperatur, Luftfeuchtigkeit und Umgebungsdruck, der Leistungsfähigkeit der eingesetzten Messtechnik (Offset, Drift) und der Kompetenz des Kalibriertechnikers abhängig.
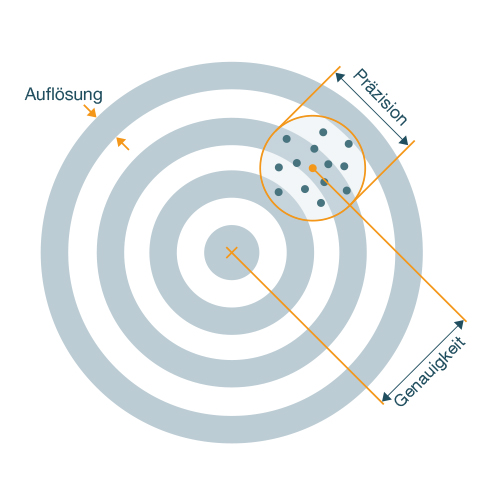
Zusammenhang zwischen: Präzision, Genauigkeit und Auflösung
Unter der Auflösung wird die kleinste Zähleinheit, hier der Abstand der Ringe der Zielscheibe, verstanden. Die Streuung der Einschusslöcher gibt die Präzision an. Sie ist ein Mass für die Reproduzierbarkeit der Treffer. Die Streuung der Einschusslöcher zum Zentrum der Zielscheibe wird durch die Genauigkeit ausgedrückt. (Es werden nur systematische Abweichungen berücksichtigt.)
Warum ist die Messunsicherheit relevant?
Um das Ergebnis einer Messung zu beurteilen und weiterzuverwenden, muss neben dem ermittelten Schätzwert der Messgrösse eine Aussage zur Qualität des Ergebnisses gemacht werden. Die Angabe der Messunsicherheit stärkt das Vertrauen in die Messergebnisse und ermöglicht den Vergleich verschiedener Messungen. Dies ist eine Grundvoraussetzung im nationalen und internationalen Warenaustausch. Es gibt zudem weitere Gründe, sich mit der Messunsicherheit zu beschäftigen. Zum Beispiel wenn die Messung Teil einer Kalibrierung ist und auf dem Kalibrierschein ausgewiesen werden muss oder wenn die Einhaltung der Genauigkeitsspezifikation eines Messgerätes zu bewerten ist. „Ein Messwert ohne Messunsicherheit ist kein vollständiges Messergebnis!“
Welche Auswirkung hat die Messunsicherheit im Rahmen der Kalibrierung?
Im Rahmen der Kalibrierung wird geprüft, ob der Sensor die spezifizierte Genauigkeit einhält. Die festgestellte Abweichung muss kleiner sein als die zulässige Abweichung. Doch auch die Kalibrierung selbst ist, so wie jede Messung, mit einer Unsicherheit belegt. Diese wird in Form der Messunsicherheit angegeben. Die Messunsicherheit setzt sich im Wesentlichen aus Fehlereinflüssen des Bedieners, des Prüflings, des Verfahrens und der Referenz zusammen. Die Messunsicherheit ist ein Mass für die zufällige Streuung des Messergebnisses und wird deshalb mit +/- angegeben. Sie muss je nach Entscheidungsregel in die Konformitätsbewertung mit einbezogen werden.
Wie wird die Messunsicherheit bestimmt und berechnet?
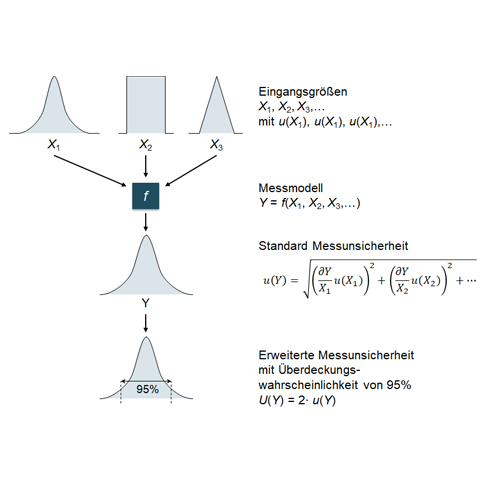
Die Ermittlung der Messunsicherheit erfolgt i.d.R. nach dem dargestellten Ablauf. Die einzelnen Einflussgrössen Xi werden entsprechend ihrer Verteilung als Wahrscheinlichkeitsfunktionen u(Xi) beschrieben, mit den zugehörigen Sensitivitäten aus dem Messmodell Y = f(Xi) verrechnet und über die Methode der quadratischen Addition zu einer Standardmessunsicherheit u(Y) kombiniert. Die Standardmessunsicherheit u(Y) ist dabei das Mass für die Streuung der Messung. Um einen Wertebereich auszudrücken, in dem der wahre Messwert mit einer Wahrscheinlichkeit von i.d.R. 95% liegt, wird die Standmessunsicherheit mit einem Erweiterungsfaktor multipliziert. In den meisten Fällen ist eine Normalverteilung zutreffend. Der Multiplikator entspricht dabei dem Zahlenwert 2.
Was bedeutet Messunsicherheit nach GUM?
Der Leitfaden „Guide to the Expression of Uncertainty in Measurement“, kurz GUM genannt, gilt als weltweit akzeptierter Standard für die Bewertung und Angaben von Messunsicherheiten und wurde von mehreren internationalen Organisationen verabschiedet. Der GUM verfolgt den Ansatz, jedes Messergebnis als besten Schätzwert einer Messgrösse mit der zugeordneten Messunsicherheit anzugeben. Somit stellt die GUM-Methode ein klar umrissenes Auswerteverfahren bereit, um die Beschreibung der Messaufgabe und die Variabilitätsbereiche von relevanten Grössen mithilfe von Wahrscheinlichkeitsverteilungen und Modellgleichungen durchzuführen. Somit kann mit Hilfe der GUM-Methode transparent gezeigt werden, welche Zusammenhänge bei der Ermittlung der Messunsicherheit benutzt werden und wie die Einschätzung von beteiligten Grössen angesehen werden.
Erfahren Sie mehr in unserer themenspezifischen Fibel:
Statistische Grundlagen für die Messunsicherheitsberechnung
Allgemein zeigt die messtechnische Erfahrung, dass Messprozesse nicht so exakt kontrolliert und Messbedingungen nicht so exakt angegeben werden können, dass einer Messgrösse nur ein einziger Wert zugeordnet werden kann. Deshalb liegt die Lösung in der Beschreibung der nicht vollständigen Kenntnisse durch Verteilungen von Werten, deren Gewicht eingeschätzt wird. Mehr oder weniger genaue Kenntnisse über verträgliche Werte einer messbaren Grösse werden durch Verteilungen der möglichen Werte beschrieben. Die Wahrscheinlichkeitsdichte bestimmt das Gewicht, das einem Wert Y der Grösse X aufgrund der vorhandenen Kenntnisse beigemessen wird. Um später eine entsprechende Messunsicherheitsberechnung durchführen zu können, sind Grundlagen der Wahrscheinlichkeitsberechnung bzw. Statistik notwendig:
Verteilungsfunktionen, wie z. B.:
- Rechteckförmige, trapezförmige, dreieckförmige, glockenförmige (Gauss'sche Glockenkurve) Verteilung
Weitere statistische Kenngrössen, wie z. B.
- Arithmetischer Mittelwert, Spannweite, Standardabweichung, Fehlerfortpflanzung
Was bedeutet Sensitivitätskoeffizient im Rahmen der Messunsicherheit?
Der Sensitivitätskoeffizient ci beschreibt, in welchem Masse der Schätzwert der Ergebnisgrösse durch Änderungen des Schätzwertes der Eingangsgrösse beeinflusst wird. Er kann aus der Modellfunktion mit Hilfe von Gleichung oder mit numerischen Methoden ermittelt werden.
Was ist eine Messunsicherheitsbilanz/ Messunsicherheitsbudget?
Die Unsicherheitsanalyse einer Messung — häufig auch Messunsicherheitsbudget genannt — sollte eine Liste aller Quellen für die Unsicherheit während der Messung zusammen mit den zugehörigen Standardmessunsicherheiten und eine Angabe enthalten, wie sie ermittelt wurden. Bei mehrfach wiederholten Beobachtungen ist auch die Anzahl n der durchgeführten Beobachtungen anzugeben.